Triangle calculator VC
The distance formula is a mathematical formula used to calculate the distance between two points in a plane. It can be used to find the length of each side of a triangle, given the coordinates of the vertices. The distance formula is:
d = √((x2 - x1)2 + (y2 - y1)2)
Where d is the distance between the two points, (x1, y1) and (x2, y2) are the coordinates of the two points.
Once you have the lengths of all three sides, you can use the Law of Cosines to find the measure of each angle in the triangle. The Law of Cosines states that:
c2 = a2 + b2 - 2ab * cos γ
where c is the length of the side opposite angle C, a and b are the lengths of the other two sides, and C is the measure of the angle opposite side c.
You can use this formula to find the measure of each angle by plugging in the known side lengths and solving for the angle.
The calculation continues of the unknown triangle parameters using the identical procedure as in the SSS triangle calculator.
Triangle in analytical problems:
- Construct 8
 Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - A triangle 6
 A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI?
A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI? - Coordinate axes
 Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y.
Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y. - Unit circle
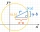 In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A.
In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - The triangle 5
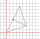 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - XY triangle
 Determine the area of a triangle given by line 2x-4y+47=0 and coordinate axes x and y.
Determine the area of a triangle given by line 2x-4y+47=0 and coordinate axes x and y. - Right triangle from axes
 A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment? - Coordinates of vector
 Determine the coordinate of a vector u=CD if C(19;-7) and D(-16;-5)
Determine the coordinate of a vector u=CD if C(19;-7) and D(-16;-5) - Intersection 74914
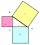 Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - X-coordinate 81737
 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Quadrant four
 Which point is located in Quadrant IV? A coordinate plane. A(-8, 6) B(-8, -6) C(8, -6) D(8, 6)
Which point is located in Quadrant IV? A coordinate plane. A(-8, 6) B(-8, -6) C(8, -6) D(8, 6) - Equation of the circle
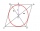 Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Points on circle
 The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose
The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose - Coordinates of midpoint
 If the midpoint of the segment is (6,3) and the other end is (8,4), what is the coordinate of the other end?
If the midpoint of the segment is (6,3) and the other end is (8,4), what is the coordinate of the other end? - Midpoint 4
 If the midpoint of a segment is (6,3) and the other endpoint is (8,-4), what is the coordinate of the other end?
If the midpoint of a segment is (6,3) and the other endpoint is (8,-4), what is the coordinate of the other end?
more triangle problems »
Also, take a look at our friend's collection of math problems and questions!
- triangle
- right triangle
- Heron's formula
- The Law of Sines
- The Law of Cosines
- Pythagorean theorem
- triangle inequality
- similarity of triangles
- The right triangle altitude theorem
