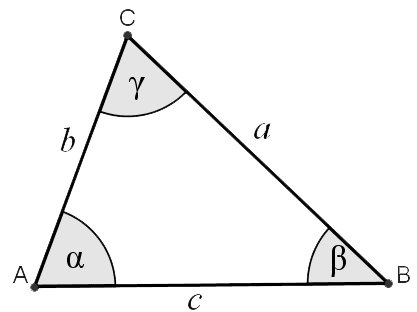
Triangle calculator
The calculator solves the triangle specified by three of its properties. Each triangle has six main characteristics: three sides a, b, c, and three angles (α, β, γ). The classic trigonometry problem is to specify three of these six characteristics and find the other three. Of course, our calculator solves triangles from combinations of main and derived properties such as area, perimeter, heights, medians, etc.
Usually by the length of three sides (SSS), side-angle-side, or angle-side-angle.
How does this calculator solve a triangle?
The calculation of the general triangle has two phases:- The expert phase is different for different tasks. The calculator tries to calculate the sizes of three sides of the triangle from the entered data. He gradually applies the knowledge base to the entered data, which is represented in particular by the relationships between individual triangle parameters.
These are successively applied and combined, and the triangle parameters are calculated. Calculator iterates until the triangle has calculated all three sides.
For example, the appropriate height is calculated from the given area of the triangle and the corresponding side. From the known height and angle, the adjacent side, etc., can be calculated. The calculator uses use knowledge, e.g., formulas and relations like the Pythagorean theorem, Sine theorem, Cosine theorem, and Heron's formula. - The second stage is the calculation of the properties of the triangle from the available lengths of its three sides.
Examples of how to enter a triangle:
a=3 b=4 c=5 ... triangle calc by three sides a,b,c.
B=45 c=10 a=9 ... triangle calc by two sides a,c and included angle B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... how to enter right-angled triangle.
a=3 β=25 γ=45 ... triangle calc if we know the side and two angles.
a=3 β=25 T=12 ... triangle calc, if know side, angle, and area of a triangle.
T=2.5 c=2 b=4 ... find side a if we know sides b, c, and the area of triangle T.
ma=1 b=2.5 c=2 ... calculation of the triangle if we know one median and any two sides.
ma=1 mb=2.5 mc=2 ... triangle calc by three medians.
ha=220, hb=165 hc=132 ... triangle calc by three heights.
a=7 β=40 mc=5 ... triangle calc by one side, one angle, and one median.
a:b:c=2:3:4 T=2.5 ... a triangle where the known side ratio and its area.
A:B:C=1:4:5 a=2 ... calculating triangle if we know the ratio of the internal angles and one side.
B=45 c=10 a=9 ... triangle calc by two sides a,c and included angle B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... how to enter right-angled triangle.
a=3 β=25 γ=45 ... triangle calc if we know the side and two angles.
a=3 β=25 T=12 ... triangle calc, if know side, angle, and area of a triangle.
T=2.5 c=2 b=4 ... find side a if we know sides b, c, and the area of triangle T.
ma=1 b=2.5 c=2 ... calculation of the triangle if we know one median and any two sides.
ma=1 mb=2.5 mc=2 ... triangle calc by three medians.
ha=220, hb=165 hc=132 ... triangle calc by three heights.
a=7 β=40 mc=5 ... triangle calc by one side, one angle, and one median.
a:b:c=2:3:4 T=2.5 ... a triangle where the known side ratio and its area.
A:B:C=1:4:5 a=2 ... calculating triangle if we know the ratio of the internal angles and one side.
What do the symbols mean?
a, b, c ... sides BC, AC, AB
A, B, C or α, β, γ ... internal angles
ha, hb, hc ... heights
ma, mb, mc ... medians
T ... area
p ... perimeter
s ... semiperimeter
Triangles in word problems:
- Triangular 82269
 A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m?
A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m? - The sides 7
 The sides of the triangle are 5.2, 4.6, and x. If the PERIMETER of the triangle is 11.2 feet, what is the length of the unknown side? (hint: draw a picture)
The sides of the triangle are 5.2, 4.6, and x. If the PERIMETER of the triangle is 11.2 feet, what is the length of the unknown side? (hint: draw a picture) - An isosceles 2
 An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame.
An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame. - Height of right RT
 The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle?
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Diagonal
 Can it be a diagonal diamond twice longer than its side?
Can it be a diagonal diamond twice longer than its side? - A triangle 10
 A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)?
A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)? - Calculate
 Calculate the area of the ABE triangle AB = 38mm and height E = 42mm Ps: please try a quick calculation
Calculate the area of the ABE triangle AB = 38mm and height E = 42mm Ps: please try a quick calculation - Intersection 64854
 Draw any triangle. Make the axis of its two sides. Their intersection is point S. (a) Measure the distance of point S from all three vertices (b) Draw the axis of the third party.
Draw any triangle. Make the axis of its two sides. Their intersection is point S. (a) Measure the distance of point S from all three vertices (b) Draw the axis of the third party. - Triangle ABC
 In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A
In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A - Diagonal
 Can a rhombus have the same length, diagonal, and side?
Can a rhombus have the same length, diagonal, and side? - Double ladder
 The double ladder is 8.5m long. It is built so that its lower ends are 3.5 meters apart. How high does the upper end of the ladder reach?
The double ladder is 8.5m long. It is built so that its lower ends are 3.5 meters apart. How high does the upper end of the ladder reach? - Sides of triangle
 The Triangle circumference with two identical sides is 117cm. The third side measures 44cm. How many cms do you measure on one of the same sides?
The Triangle circumference with two identical sides is 117cm. The third side measures 44cm. How many cms do you measure on one of the same sides? - Areaf of ST
 It is given square DBLK with side |BL|=13. Calculate the area of the triangle DKU if vertex U lies online LB.
It is given square DBLK with side |BL|=13. Calculate the area of the triangle DKU if vertex U lies online LB. - Similarity of triangles
 If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place.
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Broken tree
 The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
more triangle problems »
Look also at our friend's collection of math problems and questions:
- triangle
- right triangle
- Heron's formula
- The Law of Sines
- The Law of Cosines
- Pythagorean theorem
- triangle inequality
- similarity of triangles
- The right triangle altitude theorem